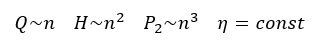
The following applies:
1. Model law
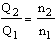
2. Model law
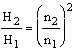
3. Model law
Q – flow rate
H – delivery head
P – power consumption
n – speed
The indices relate to the respective speed.
The affinity laws apply exactly to frictionless, incompressible flows. For technical applications, they are to be regarded as an approximate solution.
In general, these affinity laws are independent of how the speed change is technically implemented. Traditionally, multi-speed functions of small and medium size pumps are realized by changing the motor windings configurations to achieve stepped speed variations. Meanwhile, these have been largely replaced by frequency converters.
Slow-running electric drives are very expensive for larger centrifugal pumps, so that reduction gears are used for these cases.
Combustion engines are used for some mobile applications. They are also variable in speed within a specified range.
The graph of the curve is shown dropping from top left to bottom right with increasing rate of flow. The slope of the curve is determined by the pump construction and particularly by the design of the impeller.
The characteristics of the pump duty curve is the inter-dependent relationship between capacity and head.
Each change of head effects a consequential variation in the rate of flow.
High rate of flow -> low head
Low rate of flow -> high head
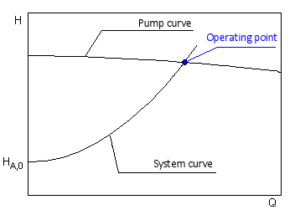
Though it is the frictional resistance of the installed pipe system which determines a given pump capacity, the respective pump can take up only one duty point on its curve. This duty point is the intersection of pump H-Q curve with the system H-Q curve.
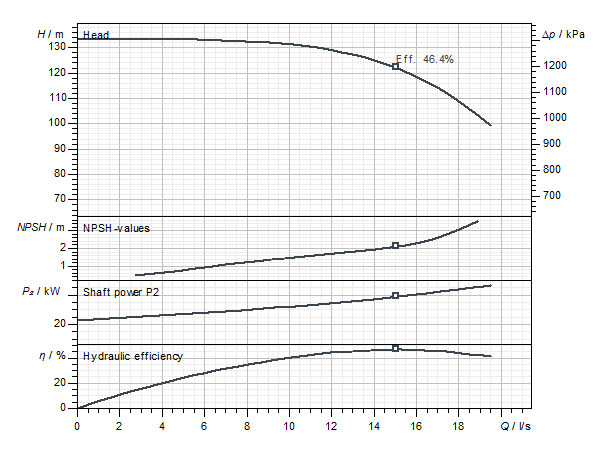
In addition to the Q-H performance curve, the following performance curves are often found for centrifugal pumps:
- Power
- Shaft power P2(Q)
- Electrical power consumption P1(Q)
- Efficiency
- Hydraulic efficiency ηhydr(Q)
- Total efficiency ηtot(Q)
- NPSH required NPSHreq(Q)
- Speed n(Q)
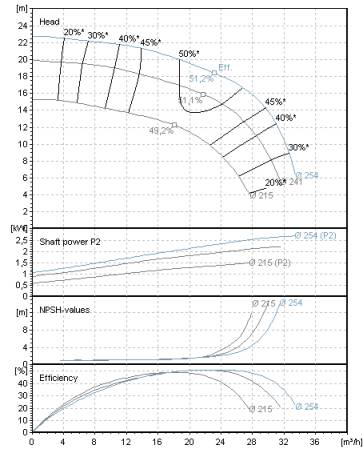
The performance curves differ in exact one parameter, such as
- Impeller diameter
- Propeller degree
- Speed
- Number of stages
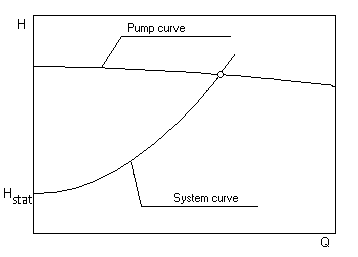
The system performance curve is composed of a static and a dynamic component.
Hsystem = Hstat + Hloss(Q)
The static component Hstat is independent of the flow velocity (and thus of the flow rate). It contains the geodetic height difference as well as the pressure difference between suction and pressure vessel or inlet and outlet point of the system under consideration. In closed circuits (e.g. heating circulation) the static heed is always zero.
The dynamic part of the performance curve describes the piping losses, which depend on the flow rate. In the case of turbulent flow of NEWTON liquids with constant loss coefficients of the system components, the characteristic curve results in a square parabola. If the static head and the duty point are known, the system curve can be shown with sufficient accuracy.
It is determined by the flow rate and head at the corresponding operating speed. When pumping highly viscous media, the pump characteristic curves and thus also the design point are shifted in relation to the characteristic curve recorded with water.
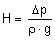
The head for the duty point of the pump is composed of
- the static head (static = independent of the flow rate)
- height difference between suction side and discharge side liquid level (geodetic head)
- pressure difference between discharge side and suction side tank (for closed tanks)
- the required outlet pressure, if any
- the friction loss head from the pressure losses in the piping system as a function of the flow rate
The useable mechanical work transferred from the pump to the fluid being pumped, related to the weight force, is called head H of the pump. At constant speed n and constant flow Q, it is independent of the density of the pumped liquid, but dependent on its viscosity.
It can be calculated by the pressure difference divided by the density of the pumped fluid and the local gravitational constant.
For Newtonian fluids one can consider the head independent from the pumped fluid for kinematic viscosities less than 20 mm²/s. By this reason it is especially suitable to present the characteristic curve of centrifugal pumps.
For pumping water the value is equal to the pressure given in meters of water column.
The maximum and minimum temperatures of the pumped medium are of particular importance for the design of the pump. They are taken into account in the selection of materials and seals and, if necessary, in a media-material resistance test.
The fluid properties (density, viscosity) change with the temperature. The power requirement of the pump is directly proportional to the density. Therefore, the temperature must be taken into account from the operating range with the maximum density. Furthermore, for viscous media (ν > 10 mm²/s), the shape of the pump performance curve must be converted.
This point is called the best efficiency point (BEP) of the pump. The position of the point changes if the hydraulic parameters of the pump, such as the impeller diameter or the speed resp. the viscosity of the pumped liquid, change.
The aim of an optimal pump selection is for the pump to operate at the BEP so that it achieves its maximum efficiency.
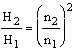 3. Model law
3. Model law
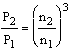 Q – flow rate
H – delivery head
P – power consumption
n – speed
The indices relate to the respective speed.
The affinity laws apply exactly to frictionless, incompressible flows. For technical applications, they are to be regarded as an approximate solution.
In general, these affinity laws are independent of how the speed change is technically implemented. Traditionally, multi-speed functions of small and medium size pumps are realized by changing the motor windings configurations to achieve stepped speed variations. Meanwhile, these have been largely replaced by frequency converters.
Slow-running electric drives are very expensive for larger centrifugal pumps, so that reduction gears are used for these cases.
Combustion engines are used for some mobile applications. They are also variable in speed within a specified range.
Q – flow rate
H – delivery head
P – power consumption
n – speed
The indices relate to the respective speed.
The affinity laws apply exactly to frictionless, incompressible flows. For technical applications, they are to be regarded as an approximate solution.
In general, these affinity laws are independent of how the speed change is technically implemented. Traditionally, multi-speed functions of small and medium size pumps are realized by changing the motor windings configurations to achieve stepped speed variations. Meanwhile, these have been largely replaced by frequency converters.
Slow-running electric drives are very expensive for larger centrifugal pumps, so that reduction gears are used for these cases.
Combustion engines are used for some mobile applications. They are also variable in speed within a specified range. 

 In addition to the Q-H performance curve, the following performance curves are often found for centrifugal pumps:
In addition to the Q-H performance curve, the following performance curves are often found for centrifugal pumps:

