Es gilt:1. Modellgesetz
2. Modellgesetz
3. Modellgesetz
Q – Förderstrom
H – Förderhöhe
P – Leistungsaufnahme
n – Drehzahl
Die Indizes beziehen sich auf die jeweilige Drehzahl.Die Affinitätsgesetze gelten exakt für reibungsfreie, inkompressible Strömungen. Für technische Anwendungsfälle sind sie als Näherungslösung zu betrachten.Generell sind diese Affinitätsgesetze unabhängig davon, wie die Drehzahländerung technisch realisiert wird. Traditionell wurde eine stufenweise Drehzahlumschaltung bei kleinen und mittleren Pumpen durch Wicklungsumschaltungen umgesetzt. Diese wurden mittlerweile weitestgehend von Frequenzumrichtern verdrängt.Für größere Kreiselpumpen sind langsam laufende elektrische Antriebe sehr teuer, so dass für diese Fälle Untersetzungsgetriebe verwendet werden.Für den mobilen Einsatz kommen außerdem Verbrennungsmotoren zum Einsatz. Diese sind ebenfalls in einem vorgegebenen Bereich drehzahlvariabel.
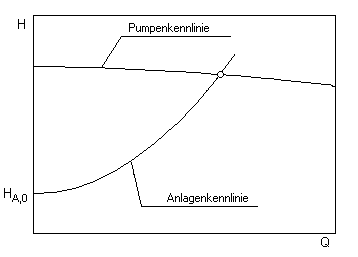
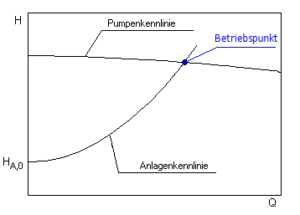
Der Verlauf der Pumpenkennlinie ist gekrümmt und fällt im Diagramm von links nach rechts mit zunehmendem Förderstrom ab. Die Neigung der Kennlinie wird durch die Konstruktion der Pumpe und insbesondere auch durch die Bauform des Laufrades bestimmt.Das Charakteristische an der Pumpenkennlinie ist die gegenseitige Abhängigkeit des Förderstromes und der Förderhöhe.Jede Änderung der Förderhöhe hat stets auch eine Änderung des Förderstromes zur Folge.Großer Förderstrom -> geringe Förderhöhe
Kleiner Förderstrom -> große FörderhöheObwohl ausschließlich das installierte Rohrleitungssystem auf Grund der Eigenwiderstände vorgibt, welcher Förderstrom bei gegebener Pumpenleistung gefördert wird, kann die betreffende Pumpe immer nur einen Betriebspunkt auf ihrer Kennlinie einnehmen. Dieser Betriebspunkt ist der Schnittpunkt der Pumpenkennlinie mit der jeweiligen Rohrnetzkennlinie.
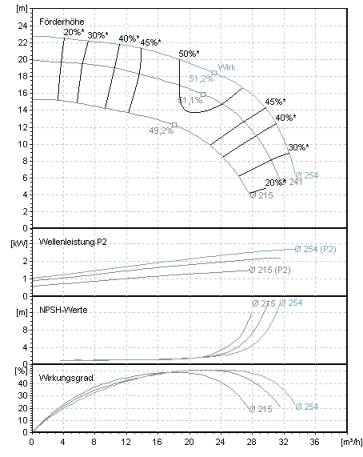
Neben der Q-H-Kennlinie sind bei Kreiselpumpen häufig folgende Kennlinien zu finden:
- Leistung
- Wellenleistung P2(Q)
- Leistungsaufnahme P1(Q) (häufig bei Tauchmotorpumpen und Nassläuferpumpen)
- Wirkungsgrad
- Hydraulischer Wirkungsgrad ηhydr(Q)
- Gesamtwirkungsgrad ηtot(Q) (häufig bei Tauchmotorpumpen und Nassläuferpumpen)
- NPSH erforderlich NPSHreq(Q)
- Drehzahl n(Q)
Die einzelnen Pumpenkennlinien unterscheiden sich in genau einem Parameter, wie z.B.
- Laufraddurchmesser
- Drehzahl
- Propellerwinkel
- Stufenanzahl
Die Anlagenkennlinie setzt sich aus einem statischen und einem dynamischen Anteil zusammen.HA = HA,0 + Hv(Q)Sie ist hauptsächlich durch die statische Höhendifferenz HGeo zwischen den Flüssigkeitsständen an Saug- und Drucktank sowie die Reibungsverluste Hv durch das gesamte Flüssigkeitsströmungssystem gekennzeichnet.Der statische Anteil HA,0 ist unabhängig von der Fließgeschwindigkeit (und somit vom Förderstrom). Er enthält den geodätischen Höhenunterschied sowie die Druckdifferenz zwischen Saug- und Druckbehälter bzw. Ein- und Austrittspunkt des betrachteten Systems. Bei geschlossenen Kreisläufen (z.B. Heizungszirkulation) ist die statische Höhe immer Null.Der dynamische Anteil der Kennlinie beschreibt die Rohrleitungsverluste, die vom Förderstrom abhängen. Bei turbulenter Strömung von NEWTONschen Flüssigkeiten mit konstanten Verlustbeiwerten der Anlagenkomponenten ergibt sich die Kennlinie zu einer quadratischen Parabel. Wenn die statische Höhe und der Sollbetriebspunkt bekannt sind, kann man daraus die Anlagenkennlinien mit hinreichender Genauigkeit darstellen.
Er wird durch den Förderstrom und die Förderhöhe bei der entsprechenden Betriebsdrehzahl bestimmt. Bei der Förderung hochviskoser Medien verschieben sich die Pumpenkennlinien und somit auch der Auslegungspunkt gegenüber der mit Wasser aufgenommenen Kennlinie.
Die Sollförderhöhe für die Auslegung der Pumpe setzt sich zusammen aus
- der statischen Höhe (statisch = unabhängig vom Förderstrom)
- Höhendifferenz zwischen saugseitigem und druckseitigem Flüssigkeitsniveau (geodätische Höhe)
- Druckdifferenz zwischen druck- und saugseitigem Behälter (bei geschlossenen Behältern)
- ggf. erforderlichem Austrittsdruck
- der Verlusthöhe aus den Druckverlusten im Rohrleitungssystem in Abhängigkeit vom Förderstrom
Die von der Pumpe auf die Förderflüssigkeit übertragene nutzbare mechanische Arbeit, bezogen auf die Gewichtskraft, nennt man Förderhöhe H der Pumpe. Sie ist bei konstanter Drehzahl n und konstantem Förderstrom Q unabhängig von der Dichte der Förderflüssigkeit, jedoch abhängig von deren Viskosität.Sie kann durch die Druckdifferenz dividiert durch die Dichte des Fördermediums und die lokale Gravitationskonstante berechnet werden.Bei newtonschen Flüssigkeiten kann die Förderhöhe unabhängig vom Fördermedium für kinematische Viskositäten unter 20 mm²/s betrachtet werden. Aus diesem Grund ist es besonders geeignet, die Kennlinie von Kreiselpumpen darzustellen.Beim Pumpen von Wasser ist der Wert der Förderhöhe gleich dem Druck in Metern Wassersäule.
Für die Auslegung der Pumpe sind insbesondere die maximale und die minimale Temperatur der Fördermediums von Bedeutung. Sie werden bei der Werkstoff- und Dichtungsauswahl und ggf. bei einer Medien-Werkstoff-Beständigkeitsprüfung berücksichtigt.Die Stoffwerte des Fördermediums (Dichte, Viskosität) ändern sich mit der Temperatur. Der Leistungsbedarf der Pumpe ist direkt proportional zur Dichte. Daher muss die Temperatur aus dem Betriebsbereich mit der maximalen Dichte berücksichtigt werden. Darüber hinaus muss bei viskosen Medien (ν > 10 mm²/s) der Verlauf der Pumpenkennlinien umgerechnet werden.
Dieser Punkt wird auch Auslegungspunkt (BEP = best efficiency point) der Pumpe genannt. Die Lage des Punktes ändert sich, wenn die hydraulischen Parameter der Pumpe, wie zum Beispiel der Laufraddurchmesser oder die Drehzahl oder die Viskosität des Fördermediums sich verändern.Ziel einer optimalen Pumpenauswahl ist es, dass die Pumpe im Auslegungspunkt arbeitet, damit sie ihren maximalen Wirkungsgrad erreicht.
2. Modellgesetz
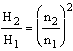3. Modellgesetz
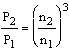Q – Förderstrom
H – Förderhöhe
P – Leistungsaufnahme
n – Drehzahl
Die Indizes beziehen sich auf die jeweilige Drehzahl.Die Affinitätsgesetze gelten exakt für reibungsfreie, inkompressible Strömungen. Für technische Anwendungsfälle sind sie als Näherungslösung zu betrachten.Generell sind diese Affinitätsgesetze unabhängig davon, wie die Drehzahländerung technisch realisiert wird. Traditionell wurde eine stufenweise Drehzahlumschaltung bei kleinen und mittleren Pumpen durch Wicklungsumschaltungen umgesetzt. Diese wurden mittlerweile weitestgehend von Frequenzumrichtern verdrängt.Für größere Kreiselpumpen sind langsam laufende elektrische Antriebe sehr teuer, so dass für diese Fälle Untersetzungsgetriebe verwendet werden.Für den mobilen Einsatz kommen außerdem Verbrennungsmotoren zum Einsatz. Diese sind ebenfalls in einem vorgegebenen Bereich drehzahlvariabel.
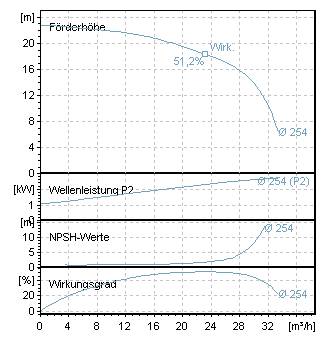
Neben der Q-H-Kennlinie sind bei Kreiselpumpen häufig folgende Kennlinien zu finden:
