Autor: al
Odtok dešťové vody QR
r 5/2 pětiminutový déšť, který je statisticky nutno očekávat jednou za 2 roky r 5/100 Pětiminutový déšť, který je statisticky nutno očekávat jednou za 100 let
Hodnoty pro řadu německých měst jsou uvedeny jako příklady v DIN 1986-100. Hodnoty se liší od r 5/2 = 200 až 250 l / (s ha) nebo r 5/100 = 800 l / (s ha) [1 ha = 10,000 m]. Informace o událostech deště lze získat od místních úřadů nebo alternativně od německé meteorologické služby. Referenční hodnoty jsou uvedeny v příloze A DIN EN 1986-100. Pokud nejsou k dispozici žádné hodnoty, mělo by se předpokládat r T (n) = 200 l / (s ha). Systémy vedení a související komponenty dešťového odvodňovacího systému je třeba z ekonomických důvodů a pro zajištění samočisticí schopnosti dimenzovat na středně silný déšť. Vypočítaný déšť je v rámci DIN 1986-100 idealizovaný déšť (blokový déšť) s konstantní intenzitou deště po dobu 5 minut. Roční počet (T n ), který se má v každém případě použít pro návrhový případ, je určen zadáním. Déšť nad vypočítaným deštěm (r 5/2 ) je třeba očekávat podle plánu.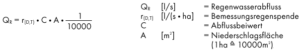
Čerpané médium v technologii odpadních vod
Při dimenzování musí být zajištěno, že pro čerpání splašků obsahujících fekálie ze šachet, které jsou napojeny na veřejnou kanalizační síť, musí být použity nevýbušné jednotky.
Viz také například UVV 54.
§2 Kanalizační síť, její přístupové body, studny, šachty a dešťové vpusti, jakož i sběrná místa a ventilační kohouty v síti tlakového potrubí jsou považovány za potenciálně výbušné jako celek…
nebo směrnice pro ochranu proti výbuchu (Ex-RL) obchodního sdružení (GUV 19.8) Vydání 06.96, sbírka příkladů, sériové číslo 7.3.1.1.
Existují však další předpisy, které je třeba vzít v úvahu. Více informací o vašem konkrétním případu získáte na živnostenském sdružení, živnostenském dozoru, TÜV nebo stavebním úřadu.
Rychlost – zákony afinity
Platí následující:
1. Modelové právo
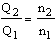2. Modelové právo
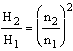3. Modelové právo
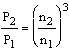Q – průtok
H – dodací hlava
P – spotřeba energie
n – rychlost
Indexy se vztahují k příslušné rychlosti.
Zákony afinity platí přesně pro toky bez tření, nestlačitelné. Pro technické aplikace je třeba je považovat za přibližné řešení.
Obecně platí, že tyto zákony afinity jsou nezávislé na tom, jak je změna rychlosti technicky implementována. Tradičně se u malých a středních čerpadel zaváděla kroková změna otáček výměnou vinutí. Ty byly mezitím z velké části nahrazeny frekvenčními měniči.
Pomaloběžné elektropohony jsou u větších odstředivých čerpadel velmi drahé, proto se pro tyto případy používají redukční převody.
Spalovací motory se používají i pro mobilní použití. Ty mají také proměnnou rychlost ve stanoveném rozsahu.
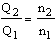2. Modelové právo
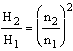3. Modelové právo
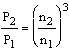Q – průtok
H – dodací hlava
P – spotřeba energie
n – rychlost
Indexy se vztahují k příslušné rychlosti.
Zákony afinity platí přesně pro toky bez tření, nestlačitelné. Pro technické aplikace je třeba je považovat za přibližné řešení.
Obecně platí, že tyto zákony afinity jsou nezávislé na tom, jak je změna rychlosti technicky implementována. Tradičně se u malých a středních čerpadel zaváděla kroková změna otáček výměnou vinutí. Ty byly mezitím z velké části nahrazeny frekvenčními měniči.
Pomaloběžné elektropohony jsou u větších odstředivých čerpadel velmi drahé, proto se pro tyto případy používají redukční převody.
Spalovací motory se používají i pro mobilní použití. Ty mají také proměnnou rychlost ve stanoveném rozsahu. Křivka čerpadla
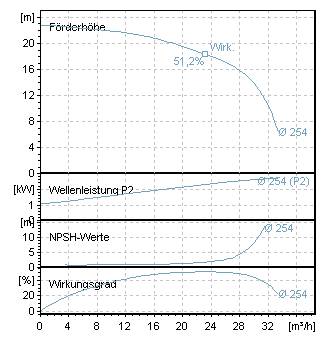
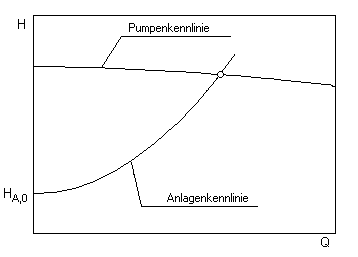
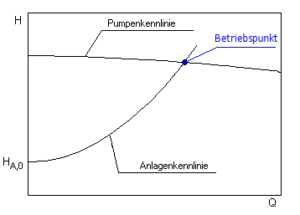
Charakteristická křivka čerpadla je zakřivená a klesá v diagramu zleva doprava s rostoucím průtokem. Sklon charakteristické křivky je určen konstrukcí čerpadla a zejména tvarem oběžného kola.
Charakteristikou křivky čerpadla je vzájemná závislost průtoku a dopravní výšky.
Každá změna dopravní výšky má vždy za následek změnu průtoku.
Velký průtok – & gt; nízká hlava
Malý průtok – & gt; velká hlava
Ačkoli pouze instalovaný potrubní systém v důsledku vlastního odporu určuje, jaký průtok je při daném výkonu čerpadla dopravován, může dané čerpadlo na své charakteristické křivce vždy zaujmout pouze jeden provozní bod. Tento pracovní bod je průsečíkem křivky čerpadla s příslušnou křivkou potrubní sítě.
Kromě charakteristiky Q-H lze u odstředivých čerpadel často nalézt následující charakteristiky:
Kromě charakteristiky Q-H lze u odstředivých čerpadel často nalézt následující charakteristiky:
- výkon
- Výkon hřídele P 2 (Q)
- Spotřeba energie P 1 (Q) (často u čerpadel s ponorným motorem a mokroběžných čerpadel)
- účinnost
- Hydraulická účinnost η hydr (Q)
- Celková účinnost η tot (Q) (často u čerpadel s ponorným motorem a čerpadel s mokrým rotorem)
- NPSH požadováno NPSH req (Q)
- Rychlost n (Q)
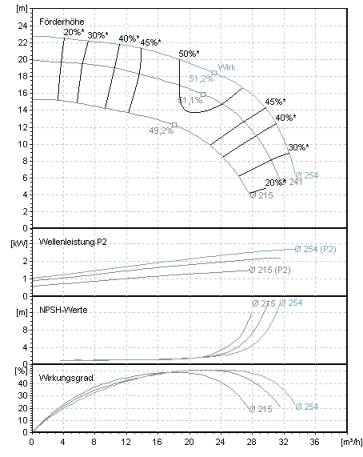
Mapa pumpy
Jednotlivé charakteristiky čerpadla se liší právě v jednom parametru, jako je kupř
- Průměr oběžného kola
- Rychlost
- Úhel vrtule
- Počet kroků
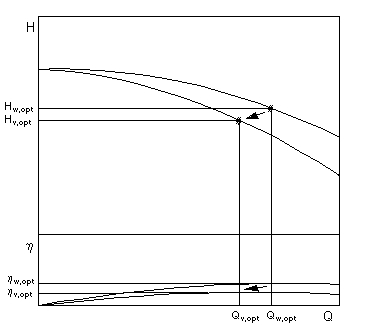
Převod charakteristické křivky pro různá média
S rostoucí viskozitou se však zvyšuje vliv REYNOLDSova čísla, takže v praxi se předpokládá, že tato aproximace je od kinematické viskozity kolem 20 mm²/s nedostatečná. K nápravě byly vyvinuty empirické metody převodu zaznamenaných charakteristik na média se střední a vysokou viskozitou, která v praktické aplikaci ve starších verzích znamenají komplexní vyhodnocení diagramů, která však v současných verzích byla připravena pomocí vhodných sad vzorců.
Celosvětově nejrozšířenější je postup z Hydraulic Institute (USA), který byl standardizován jako ANSI/HI 9.6.7 a ISO/TR 17766.
V praxi se dnes konverze většinou provádí pomocí počítačových programů, jako je Spaix PumpSelector. Počítačově technické provedení tohoto postupu umožňuje převod charakteristických křivek, přičemž uživatel musí pouze definovat požadovaná dopravní data a dopravní médium. U všech známých metod hraje konstrukční bod čerpadla zvláštní roli při převodu charakteristických křivek.
Pro platnost postupu lze stanovit následující podmínky:
- Odstředivá čerpadla s uzavřenými nebo polootevřenými oběžnými koly
- Kinematická viskozita v rozsahu mezi 1 a 3000 mm²/s
- Průtok v nejlepším provozním bodě mezi 3 a 410 m³/h
- Výška na krok mezi 6 a 130 m
- Výroba za normálních provozních podmínek
- Přeprava kapalin NEWTON
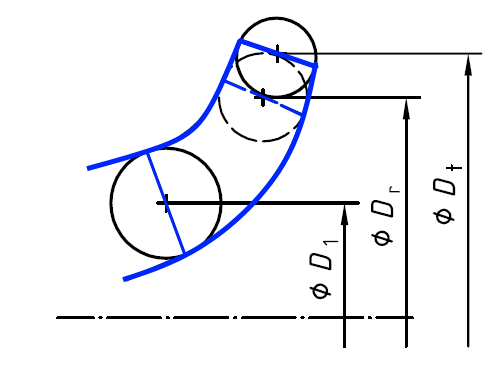
Přepočet charakteristické křivky při otáčení oběžného kola
Přibližně platí:
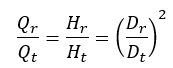Q = průtok
H = dopravní hlava
D = průměr oběžného kola
r = index pro zmenšený průměr oběžného kola
t = index pro průměr referenčního kola
Z tohoto vztahu lze zhruba určit křivku škrticí klapky H (Q).
Přesnější výpočet však vyžaduje zohlednění charakteristických map, ve kterých je každé charakteristické křivce přiřazen průměr oběžného kola. Nový průběh charakteristiky je určen interpolací převodu ze sousedních charakteristik. Pro plné využití efektivity procesu se doporučuje zaznamenat mapu oběžného kola s minimálně třemi charakteristickými křivkami. Pokud existuje velký kalibrační rozdíl mezi nejmenším a největším průměrem oběžného kola, jsou vyžadovány některé (2..4) mezilehlé charakteristiky.
Alternativní metoda výpočtu je popsána v ISO 9906. Je nutné znát střední průměr oběžného kola na náběžné hraně D 1 . Tento postup je dle normy platný pro
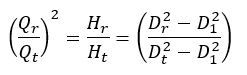D 1 = Střední průměr na náběžné hraně oběžného kola
U čerpadel s typovým číslem K ≤ 1,0 a maximálním zmenšením průměru oběžného kola o 3 % lze účinnost považovat za konstantní.
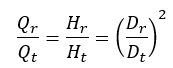Q = průtok
H = dopravní hlava
D = průměr oběžného kola
r = index pro zmenšený průměr oběžného kola
t = index pro průměr referenčního kola
Z tohoto vztahu lze zhruba určit křivku škrticí klapky H (Q).
Přesnější výpočet však vyžaduje zohlednění charakteristických map, ve kterých je každé charakteristické křivce přiřazen průměr oběžného kola. Nový průběh charakteristiky je určen interpolací převodu ze sousedních charakteristik. Pro plné využití efektivity procesu se doporučuje zaznamenat mapu oběžného kola s minimálně třemi charakteristickými křivkami. Pokud existuje velký kalibrační rozdíl mezi nejmenším a největším průměrem oběžného kola, jsou vyžadovány některé (2..4) mezilehlé charakteristiky.
Alternativní metoda výpočtu je popsána v ISO 9906. Je nutné znát střední průměr oběžného kola na náběžné hraně D 1 . Tento postup je dle normy platný pro
-
- Snížení průměru až o max. 5 %
- Zadejte číslo K ≤ 1,5
- nezměněná geometrie čepele (výstupní úhel, kužel atd.) po otočení
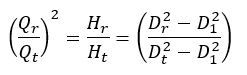D 1 = Střední průměr na náběžné hraně oběžného kola
U čerpadel s typovým číslem K ≤ 1,0 a maximálním zmenšením průměru oběžného kola o 3 % lze účinnost považovat za konstantní. Výpočet charakteristiky systému
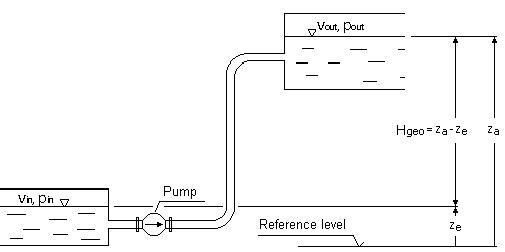
Potřebná dopravní výška čerpadla v nerozvětveném potrubí se získá z BERNOULLIHO rovnice pro jednorozměrné, stacionární proudění nestlačitelného média:
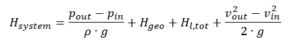p in , p out = tlaky při nasávání nebo vypouštění hladin kapaliny
ρ = hustota kapaliny
g = tíhové zrychlení (9,81 m/s²)
H geo = statický výškový rozdíl mezi hladinou kapaliny v nádobách na sací a výtlačné straně
H l, tot = celková ztráta potrubí třením mezi vstupem a výstupem
v in , v out = střední průtokové rychlosti v sacích a výtlačných nádobách
Podle zákona kontinuity jsou střední rychlosti proudění v sacích a výtlačných nádržích většinou nevýznamně malé a lze je zanedbat, pokud jsou povrchy nádrží relativně velké ve srovnání s povrchy potrubí. V tomto případě je výše uvedený vzorec zjednodušený na:
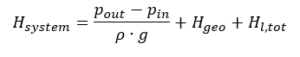Statická část charakteristiky systému, tedy ta část, která nezávisí na rychlosti proudění a tedy na průtoku, je:
U uzavřených systémů je tato hodnota nulová.
Celková ztrátová částka je tvořena ztrátami všech součástí sacího a tlakového potrubí. S dostatečně velkými REYNOLDSOVÝMI čísly je úměrná druhé mocnině objemového průtoku.
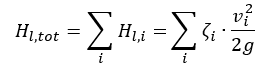
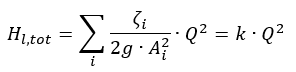g = tíhové zrychlení (9,81 m/s²)
H l, tot = celková ztráta třením mezi vstupem a výstupem
v i = střední rychlosti proudění přes plochu průřezu potrubí i
A i = charakteristická plocha průřezu potrubí
ζ i = koeficient ztráty třením pro trubky, tvarovky atd.
Q = průtok
k = faktor proporcionality
Za uvedených podmínek lze nyní specifikovat parabolu charakteristiky systému:
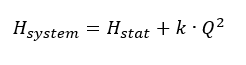Faktor úměrnosti k se určí z požadovaného pracovního bodu. Průsečík charakteristiky systému s křivkou škrticí klapky specifickou pro čerpadlo (charakteristika čerpadla) představuje skutečný provozní bod.
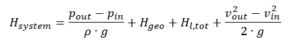p in , p out = tlaky při nasávání nebo vypouštění hladin kapaliny
ρ = hustota kapaliny
g = tíhové zrychlení (9,81 m/s²)
H geo = statický výškový rozdíl mezi hladinou kapaliny v nádobách na sací a výtlačné straně
H l, tot = celková ztráta potrubí třením mezi vstupem a výstupem
v in , v out = střední průtokové rychlosti v sacích a výtlačných nádobách
Podle zákona kontinuity jsou střední rychlosti proudění v sacích a výtlačných nádržích většinou nevýznamně malé a lze je zanedbat, pokud jsou povrchy nádrží relativně velké ve srovnání s povrchy potrubí. V tomto případě je výše uvedený vzorec zjednodušený na:
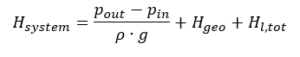Statická část charakteristiky systému, tedy ta část, která nezávisí na rychlosti proudění a tedy na průtoku, je:
U uzavřených systémů je tato hodnota nulová.
Celková ztrátová částka je tvořena ztrátami všech součástí sacího a tlakového potrubí. S dostatečně velkými REYNOLDSOVÝMI čísly je úměrná druhé mocnině objemového průtoku.
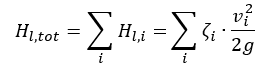
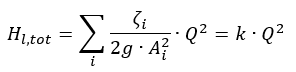g = tíhové zrychlení (9,81 m/s²)
H l, tot = celková ztráta třením mezi vstupem a výstupem
v i = střední rychlosti proudění přes plochu průřezu potrubí i
A i = charakteristická plocha průřezu potrubí
ζ i = koeficient ztráty třením pro trubky, tvarovky atd.
Q = průtok
k = faktor proporcionality
Za uvedených podmínek lze nyní specifikovat parabolu charakteristiky systému:
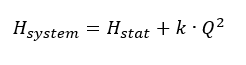Faktor úměrnosti k se určí z požadovaného pracovního bodu. Průsečík charakteristiky systému s křivkou škrticí klapky specifickou pro čerpadlo (charakteristika čerpadla) představuje skutečný provozní bod.
Charakteristika systému
Charakteristika systému se skládá ze statické a dynamické části.
H A = H A, 0 + H v (Q)
Vyznačuje se především statickým výškovým rozdílem H Geo mezi hladinami kapalin v sacích a tlakových nádržích a ztrátami třením H v v celém systému proudění kapaliny.
Statická složka H A, 0 je nezávislá na průtoku (a tedy na průtoku). Obsahuje geodetický výškový rozdíl i rozdíl tlaků mezi sací a tlakovou nádobou nebo vstupním a výstupním bodem uvažovaného systému. U uzavřených okruhů (např. cirkulace topení) je statická výška vždy nulová.
Dynamická část charakteristiky popisuje ztráty potrubí, které závisí na průtoku. V případě turbulentního proudění kapalin NEWTON s konstantními ztrátovými součiniteli komponent systému je výsledkem charakteristická křivka kvadratická parabola. Pokud je známa statická výška a cílový pracovní bod, lze charakteristiky systému zobrazit s dostatečnou přesností.