Schlagwort: NEWTONsche Flüssigkeit

Kennlinienumrechnung für verschiedene Medien

Posted on von bs
Mit zunehmender Viskosität steigt jedoch der REYNOLDS-Zahl-Einfluss, so dass man in der Praxis davon ausgeht, dass diese Näherung ab einer kinematischen Viskosität von etwa 20 mm²/s ungenügend ist. Zur Korrektur wurden für die Umrechnung der aufgenommenen Kennlinien auf mittel- und hochviskose Medien empirisch Verfahren entwickelt, die in der praktischen Anwendung in älteren Versionen die aufwendige Auswertung von Diagrammen bedeuten, in den aktuellen Versionen jedoch durch entsprechende Formelsätze aufbereitet wurden. Weltweit am meisten verbreitet ist das Verfahren vom Hydraulic Institute (USA), welches als ANSI/HI 9.6.7 und ISO/TR 17766 standardisiert wurde. 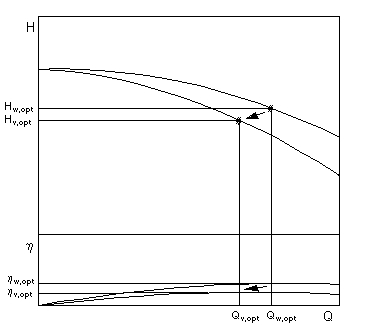Praktisch wird die Umrechnung heute meist durch Computerprogramme wie dem Spaix PumpSelector vorgenommen. Die computertechnische Umsetzung dieses Verfahrens ermöglicht die Umrechnung von Kennlinien, wobei vom Anwender nur die gewünschten Förderdaten und das Fördermedium zu definieren sind. Eine spezielle Rolle bei der Umrechnung von Kennlinien spielt bei allen bekannten Verfahren der Auslegungspunkt der Pumpe. Folgende Bedingungen können für die Gültigkeit des Verfahrens angegeben werden:
  • Kreiselpumpen mit geschlossenen oder halboffenen Laufrädern
  • Kinematische Viskosität im Bereich zwischen 1 und 3000 mm²/s
  • Förderstrom im Bestbetriebspunkt zwischen 3 und 410 m³/h
  • Förderhöhe pro Stufe zwischen 6 und 130 m
  • Förderung unter normalen Betriebsbedingungen
  • Förderung von NEWTONschen Flüssigkeiten

Viskosität

Posted on von bs
In NEWTONschen Flüssigkeiten entstehen bei laminaren Strömungsvorgängen Schubspannungen und dem Druck überlagerte Normalspannungen, die der Deformationsgeschwindigkeit proportional sind, wobei der Proportionalitätsfaktor die dynamische Viskosität ist. Die kinematische Viskosität ist definiert als: Die Viskosität ist temperatur- und druckabhängig, wobei die Druckabhängigkeit bei Flüssigkeiten vernachlässigbar klein ist. Bei nicht-NEWTONschen Flüssigkeiten kann die Viskosität außerdem zeitabhängig sein (thixotropes bzw. rheopexes Fließverhalten). Sie ist dann nicht mehr als Stoffwert angebbar. Die Viskosität eines Mediums hat sowohl einen Einfluss auf die Rohrleitungskennlinie als auch auf die Pumpenkennlinie. Für Kreiselpumpen werden die Pumpenkennlinien in der Praxis bei einer kinematischen Viskosität von über 10 mm²/s umgerechnet.

Nicht-NEWTONsche Flüssigkeiten

Posted on von bs
Dies ist dadurch gekennzeichnet, dass ein linearer Zusammenhang zwischen Deformations- und Spannungstensor nicht gegeben ist und/oder dass die Viskosität zeitabhängig ist. Nicht-NEWTONsches Fließverhalten kann z. B. bei folgenden Medien beobachtet werden:
  • Gasruß in Ölfirnis
  • Getreidekornsuspension in Wasser
  • Abwasserschlamm
  • Fäkalien
  • Zahnpasta
  • Mörtel
  • Seifenlösungen
Beispiele: Bei zahlreichen Farben und Lacken lässt sich ein thixotropes Verhalten beobachten, d. h. die Viskosität ist zeitabhängig. Beim Rühren mit konstanter Winkelgeschwindigkeit lässt sich zunächst ein sehr großer Widerstand beobachten, während nach einiger Zeit die Viskosität deutlich abnimmt und gegen einen unteren Grenzwert strebt. Viele industrielle Schlämme z. B. Suspensionen von Kalk (Mörtel) und Kreide (Zahnpasta) zeigen viskoplastisches Verhalten. Unterhalb der Fließspannung (Fließgrenze) verhalten sie sich wie Festkörper und darüber hinaus wie Fluide. Lösungen und Schmelzen vieler hochpolymerer Stoffe sowie Suspensionen mit länglichen Partikeln wie Kautschuke und Seifenlösungen verhalten sich strukturviskos. Die Viskosität dieser Fluide nimmt mit steigender Schergeschwindigkeit ab. Das umgekehrte Verhalten (dilatantes Verhalten) findet man z.B. bei einigen hochkonzentrierten Suspensionen. Hier steigt die Viskosität mit zunehmender Schergeschwindigkeit. Sowohl die Pumpenkennlinien als auch die klassischen Verfahren für die Rohrleitungsberechnung gehen von einer konstanten Viskosität aus und besitzen für Nicht-Newtonsche Flüssigkeiten keine Gültigkeit. In Abhängigkeit vom Fließverhalten des Fördermediums können sie bestenfalls als Näherung verwendet werden. Für viele Nicht-Newtonsche Medien gibt es deshalb spezielle Berechnungs- oder Näherungsverfahren für die Auslegung.