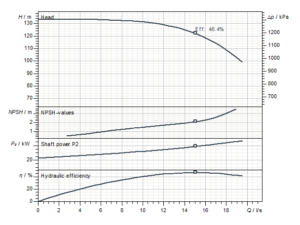
Calculating the System H-Q Curve
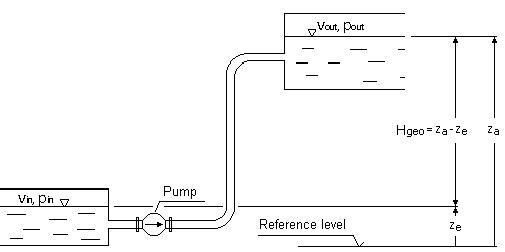
The required pumping head in a branchless pipeline is determined from BERNOULLI’s equation for one-dimensional, stationary flow of incompressible fluids:
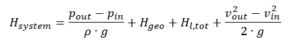
pin, pout = pressures on suction respectively discharge liquid levels
ρ = fluid density
g = gravity (9.81 m/s2)
Hgeo = static height difference between suction and discharge liquid levels
Hl,tot = total pipe friction loss between inlet and outlet areas
vin, vout = mean flow velocities at inlet and outlet liquid level areas
The mean flow velocities at the inlet and outlet areas are, based on the Continuity Law, mostly insignificantly small and can be neglected, if the tank areas being relatively large compared to those of the pipe work. In this case, above formula will be simplified to:
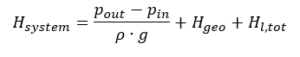
The static portion of the system H-Q curve, that part that is unrelated to the rate of flow, reads:
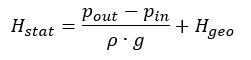
For closed circulating systems this value becomes zero.
The total friction losses are the sum of the frictional losses of all components in the suction and delivery piping. They vary, at sufficiently large REYNOLDS numbers, as the square of the flow rate.
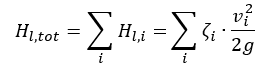
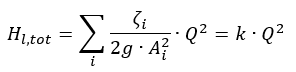
g = gravity (9.81 m/s2)
Hl,tot = total friction loss between inlet and outlet areas
vi = mean flow velocities trough pipe cross-section area
Ai = characteristic pipe cross-sectional area
ζi = friction loss coefficient for pipes, fittings, etc.
Q = flow rate
k = proportionality factor
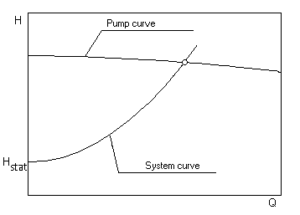
Under the above stated premises the parabolic system H-Q curve can now be drawn:
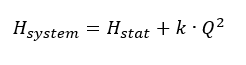
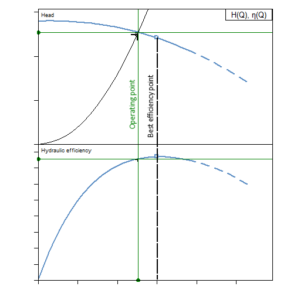
The proportionality factor k is determined of the specified duty point. The intersection of the system H-Q and the pump H-Q curves defines the actual operating point.